Neural probabilistic language model (nplm)
안녕하세요, 이번 포스팅에서는 Neural Probabilistic Language Model(NPLM)에 대해서 공부하고자 합니다. NPLM은 2003년에 AI 4대천왕 중 한분인 Yoshua Bengio 교수님께서 제안하셨고, 당시 많은 주목을 받았습니다.
논문 발표 당시 (2003)의 최신 기법은..?
2003년 당시의 최신 기법은 통계적 언어 모델 (Statistical Language Model, SLP) 하나인 n-gram 기법이었습니다. n 개의 단어들 중 앞의 첫번째부터 n-1번째까지의 단어가 주어졌을 때 마지막 n번째를 학습한 데이터의 통계 기반으로 예측하는 기법입니다.
예를 들어 ‘가는 말이 고와야 오는 말도 ___‘ 라는 문장이 있다고 합시다. 빈칸에 들어갈 말은 ‘곱다’가 되겠죠. n=3인 tri-gram 모델에서는 ‘곱다’ 라는 단어를 예측하기 위해 ‘오는’, ‘말도’ 2개의 단어만을 참고합니다. 이를 수식으로 일반화하여 나타내면 아래와 같습니다.
\[P( w_{t} | w_{t-(n-1)},...,w_{t-1}) = \frac{exp(y_{w_{t}})}{\Sigma_{i}exp(y_{i})}\]t번째 단어를 예측하기 위해서는, t번째 단어 앞에 있는 n-1개의 단어들이 주어졌을 때 가장 다음으로 올 법한 단어를 통계적으로 찾는 것입니다. 이 조건부 확률을 최대화하는 방향으로 학습하게 되면, ‘오는’, ‘말도’ 두 단어가 주어졌을 때, 수많은 단어들 중 ‘곱다’에 대해서 가장 높은 확률값을 나타내게 되는 것입니다.
N-gram의 단점과 NPLM에서 제안한 개선 방법
n-gram모델은 당시 최신 기법이었지만 몇 가지 단점들이 있었습니다.
- 참고한 n-1개의 단어가 Corpus에 존재하지 않을 때 조건부 확률이 0이 되는 점
- 차원의 저주 (Curse of dimensionality) : n을 크게 설정할수록 단어가 corpus에 존재하지 않을 확률이 증가하고, 데이터가 sparse해지는 점
- 단어 및 문장 간 유사도를 계산할 수 없다는 점.
기존의 n-gram은 컴퓨터에게 단어를 인식시키기 위해 하나의 요소만 1이고 나머지는 0인 vector로 변환하는 one-hot encoding 방법을 사용했습니다. 예를 들어서 ‘빨간’, ‘사과는’, ‘맛있다’ 이렇게 3가지 단어에 one-hot encoding을 하면 아래와 같이 변환됩니다.
‘빨간 ‘ = [0 0 1]
‘사과는’ = [0 1 0]
‘맛있다’ = [1 0 0]
겉보기엔 아주 간결하고 쉽게 표현이 되는 것 같지만, 만약 단어의 수가 아주 많아진다면 어떻게 될까요?
변환된 데이터는 차원의 수는 아주 크지만 거의 대부분이 0인 sparse vector가 됩니다.
이렇게 되면 메모리(저장공간)도 부족하고 계산 복잡도도 걷잡을 수 없이 늘어나게 되겠죠.(위에서 언급한 2번째 단점)
또 다른 단점이 있습니다. One-hot vector들은 자신의 고유한 차원에서만 1의 값을 가지고 나머지 차원에서는 모두 0을 가지므로 서로 내적(inner product)를 하면 항상 0이 나오는데요, 두 벡터간의 내적이 0이면 두 벡터는 서로 직교(orthogonal)합니다. 즉, one-hot vector는 서로 직교(orthogonal)하므로 각각 독립이 됩니다. 실제로 단어들 간에는 여러가지 연관성(품사, 유의어, 동의어 등)을 가질 수 있지만, one-hot vector로 표현하면 모든 단어를 서로 독립으로 간주하기 때문에 이러한 단어 간의 연관성을 담아내지 못합니다.
물론 NPLM 이전에도 n-gram의 단점들을 보완하기 위해서 back-off나 smoothing 같은 방법이 제안되기도 했었습니다만 (자세한 내용은 수박바 님의 블로그를 참고해주세요),
NPLM에서는 이러한 문제점들을 해결하기 위해 분산 표현 (Distributed Representation)이라는 개념을 제안합니다.
one-hot vector보다 훨씬 적은 m차원의 vector에 모든 요소가 실수로 채워진 형태인데요, 초기값은 랜덤한 실수로 구성되어 있지만 학습을 통해 각 벡터들은 점점 각 단어의 정보를 압축하는 벡터가 됩니다. 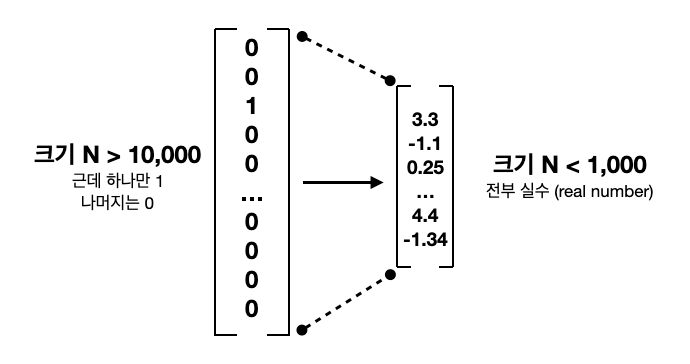
이처럼 NPLM에서는 one-hot vector와 같은 sparse 벡터 대신 밀집 벡터(Dense vector)로 임베딩(Embedding)하여 차원의 저주 (Curse of dimensionality)를 해결하고, 모든 n-gram을 저장하지 않아도 되기 때문에 기존 n-gram 언어 모델보다 저장 공간의 이점을 가지며, 단어의 유사도를 표현 할 수 있습니다. 학습이 잘 완료된 dense vector를 아래 그림에서 한번 살펴 볼까요?
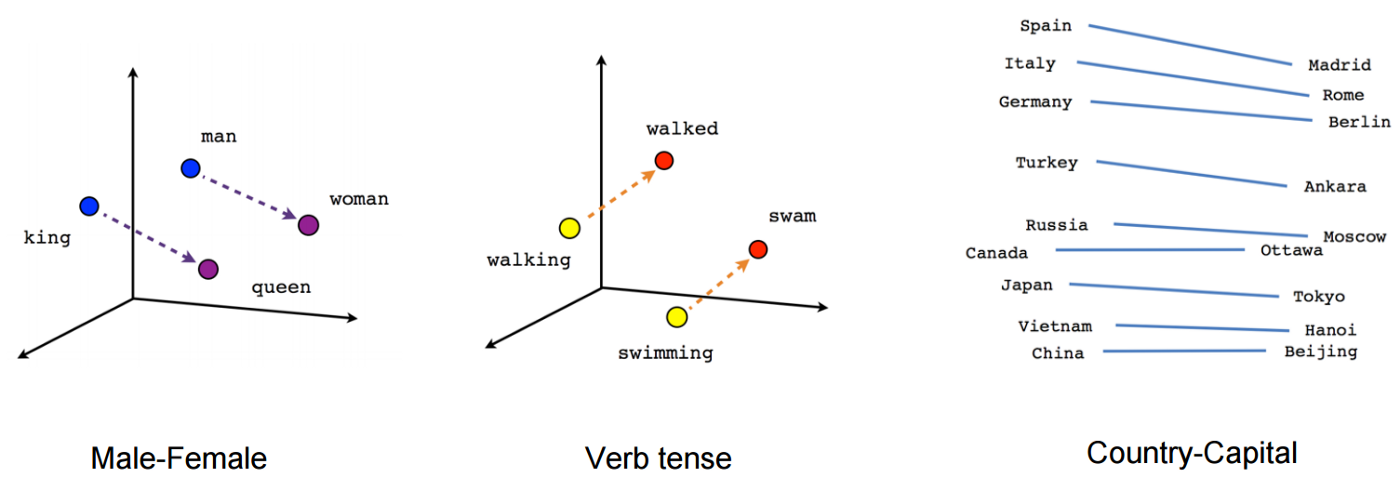
신기하게도 성별, 단어의 속성, 국가-수도 관계에 대한 방향성 등이 아주 잘 반영되어 있는 것을 확인할 수 있습니다.
NPLM Model
자, 그럼 지금부터 본격적으로 NPLM에 대한 모델을 살펴 볼까요?
아래에 있는 그림이 NPLM의 모델을 나타냅니다.
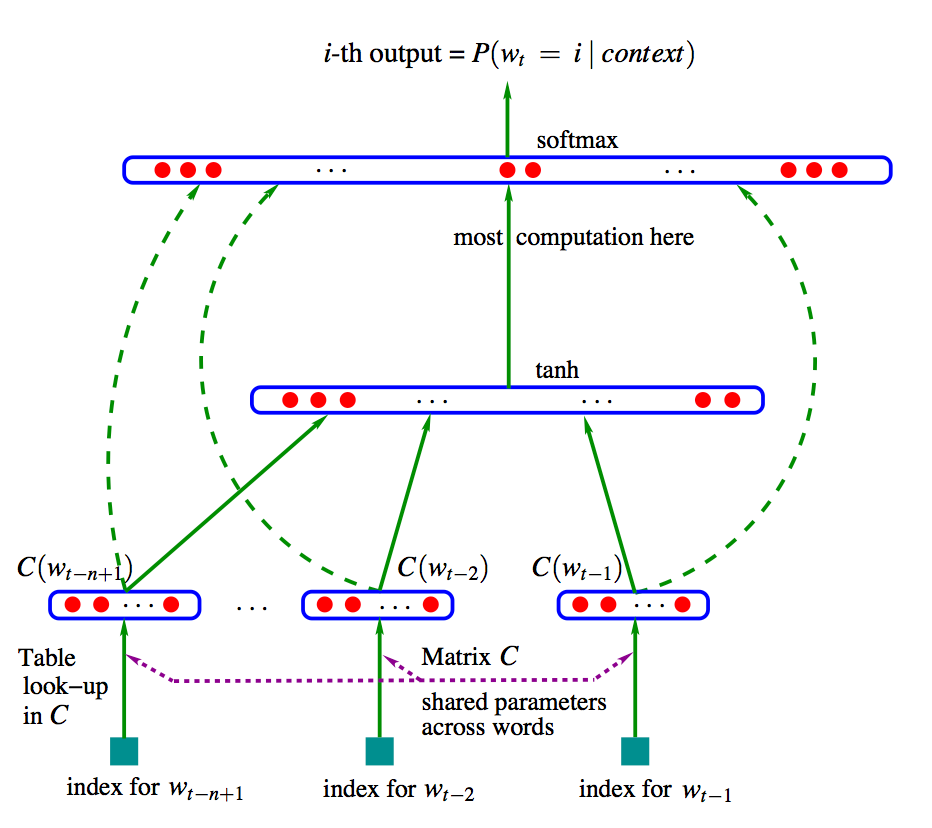
NPLM에서 target을 예측하기 위한 output 수식은 $Y_{w_{t}} = b + Wx_{t} + U( tanh(Hx_{t}+d) )$ 입니다.
Parameters
V : 총 토큰(단어) 개수
m : 임베딩 벡터 차원 (단어를 몇 차원의 벡터로 임베딩할건지 결정. 예를 들어 m=2이면 2차원의 벡터가 생성됨)
n_hidden : hidden layer의 unit 수
C (Embedding matrix) : 각 인덱스에 있는 단어가 embedding되어 vector 형태로 들어 있음. 차원 = V x m
H : Embedding matrix와 hidden layer 사이의 weight. 차원 = ( (n-1) * m ) x n_hidden
d : hidden layer의 bias. 차원 = n_hidden
U : hidden layer가 activation function (tanh)까지 거친 후와 output 사이의 weight. 차원 = n_hidden x V
W : Embedding layer에서 output까지 직접 연결하기 위한 weight. 차원 = ( (n-1) * m ) x V
b : 가장 마지막에(out 직전에) 더해주는 bias.
$w_{t}$ : 문장에서 t번째 단어
$x_{t}$ : 문장에서 t번째 단어가 C (Embedding matrix)를 거쳐 임베딩 된 형태. C($w_{t}$)와 동일
from INPUT to OUTPUT
우선, 인풋 단위부터 살펴 보겠습니다.
NPLM은 n-gram 기반 모델이기 때문에 n개의 단어 중 첫번째부터 n-1번째 까지의 단어가 input으로 사용되며, 마지막 n번째 단어가 target으로 사용됩니다.
위의 모델 그림에서는 $w_{t}$가 target이라고 했을 때, $w_{t-n+1}$부터 $w_{t-1}$까지 n-1개의 단어가 C (Embedding layer) 에서 Table look-up을 통해 임베딩 되는 것을 확인할 수 있습니다. 여기서 Table look-up 이란, 각 단어들의 Embedding vector들을 모아놓은 C layer에서 자신의 index에 해당하는 embedded vector를 가져오는 것을 말하는데요, 아래 그림처럼 총 4개의 단어가 5차원의 벡터로 embedding되어 있다고 가정하면, 3번째 단어는 embedding matrix에서 3번째 행만 가지고 오면 되는 것이죠.
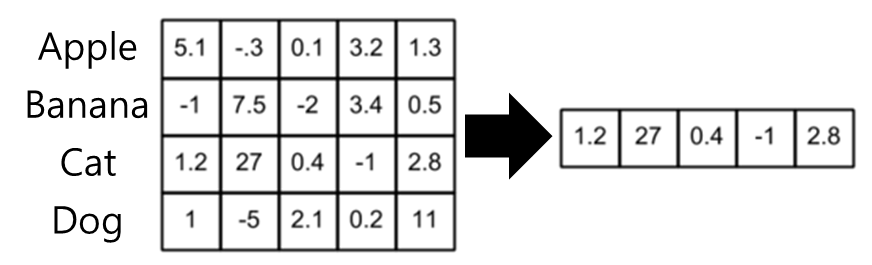
C (Embedding matrix)를 거친 단어($w$)들은 $x$가 되고, 다음으로 $H$ weight와 곱해진 후 bias ($d$)가 더해집니다 ($Hx_{t} + d$).
다음으로, activation function인 tanh 함수를 거치게 되면 위의 모델 그림에서 중앙에 위치한 레이어가 됩니다 ( $tanh(Hx_{t} + d)$ ).
다음 레이어로 가면서 $U$ weight와 곱해진 후, bias ($b$)가 더해지게 됩니다. ( $b + U( tanh(Hx_{t} + d)$ )
그런데, 수식을 보면 $W$라는 term이 하나 더 있네요. 원문에서 W는 embedding layer에서 output layer까지 직접적인 연결 (direct connection)이라고 말합니다. 모델 그림에서는 초록색 점선에 해당합니다. 만약 embedding layer와 output layer의 직접적인 연결을 원한다면 $W$를 실수로 두고, 그렇지 않다면 $W$를 0으로 두면 되는 것이죠.
따라서 embedded vector인 $x_{t}$를 $W$ weight와 곱한 것까지 더해주면 최종 output에 대한 식이 완성됩니다
( $b + Wx_{t} + U( tanh(Hx_{t} + d)$ ).
이렇게 예측된 output값은 softmax를 거친 후에 확률로 변환이 되며, cross-entropy를 이용하여 cost를 계산할 수 있습니다. 마지막으로 adam과 같은 optimizer를 이용하여 backpropagation과 weight를 업데이트 해주면 되겠네요.
마치며
이번 포스팅에서는 n-gram 기반의 모델을 dense vector (밀집 벡터)를 활용하여 크게 개선한 Nerual Probability Language Model에 대해서 공부했습니다. 그럼에도 불구하고, NPLM은 학습해야할 parameter가 너무 많아 연산을 많이 해야한다는 단점이 있습니다. 이는 2013년 Word2Vec이 제안되면서 또다시 크게 개선됩니다. 그럼에도 불구하고 NPLM은 혁신적인 word embedding을 이용해서 현재 기술들에 아주 중요한 초석이 된 것 같습니다.
다음 포스팅에서는 여기서 공부한 NPLM을 직접 pytorch를 기반으로 구현을 해보도록 하겠습니다.

Comments