Word2vec 1편 개념부터 weight update까지
안녕하세요, 이번 포스팅에서는 Word2Vec에 대해서 공부하고자 합니다. Word2Vec은 구글에서 2013년에 발표한 word embedding 방법 중 하나로, 이름에서도 알 수 있듯이 단어를 벡터로 바꿔준다는 (Word to Vector) 의미를 가지고 있습니다. Word2Vec은 특히 단어 간 유사도와 관계를 잘 나타내서 큰 주목을 받았고, 지금은 word embedding의 역사에 한 획을 그었다고 해도 무방할 정도로 유명한 기법이 되었습니다.
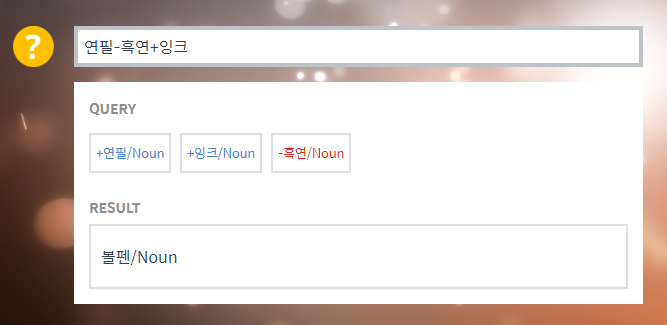
Word2Vec으로 단어들을 학습시키면 컴퓨터는 아래 그림과 같이 ‘연필 - 흑연 + 잉크 = 볼펜’ 이라는 답을 합니다. 연필에서 흑연을 빼고 잉크를 채워넣으면 볼펜이 된다는 것을 컴퓨터가 이해하고 대답할 수 있다는 것이 정말 놀랍지 않나요? 다른 예제로 테스트를 해보고 싶으시다면 이 곳에서 해보실 수 있습니다.
Word embedding과 Neural Probabilistic Language Model (NPLM)
예전에는 컴퓨터에게 단어를 인식시키기 위해서 하나의 요소만 1이고 나머지는 0인 vector로 변환하는 one-hot encoding 방법을 사용했습니다. 예를 들어서 ‘빨간’, ‘사과는’, ‘맛있다’ 이렇게 총 3가지 단어가 있다면 아래와 같이 변환되었죠.
‘빨간 ‘ = [0 0 1]
‘사과는’ = [0 1 0]
‘맛있다’ = [1 0 0]
그런데 one-hot encoding 방식은 단어 개수가 많아질수록 차원의 저주(Curse of dimensionality) 문제가 생기고, 벡터 간 독립성으로 인해 단어 연관성을 표현하지 못하는 등 여러 단점이 있었습니다. 이를 해결하기 위해 2003년에 Bengio 교수님께서 Neural Probabilistic Language Model (NPLM)을 제안하셨습니다. NPLM을 처음 보시는 분이거나 one-hot vector 사용 시 단점 등 word embedding에 대해 더 자세한 설명이 필요하신 분들은 위의 링크를 타고 들어가셔서 먼저 읽어보시기를 적극 권장 드립니다!
Word2Vec vs NNLM
NPLM가 발표된 후 이보다 발전된 RNNLM, BiLM 등의 뉴럴 네트워크 기반 모델들이 발표되었는데요. 최근에는 이런 모델들을 피드 포워드 신경망 언어모델 (Feed Forward Neural Network Language Model, 줄여서 NNLM) 이라고 부릅니다. NPLM은 NNLM의 시초가 된 것이죠.
Word2Vec은 NNLM의 단점이었던 많은 연산량을 개선하기 위해서 Hidden state를 과감하게 제거했습니다.
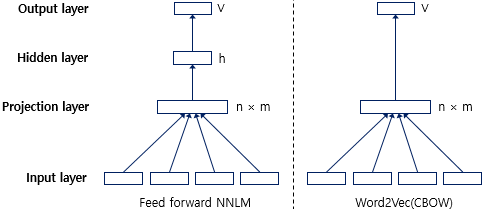
추가로, Word2Vec이 NNLM보다 훨씬 빠른 학습속도를 보이는 이유는 단지 Hidden layer를 제거했기 때문만은 아닙니다. Word2Vec에서는 연산량을 더욱 줄이기 위해서 계층적 소프트맥스 (Hierarchical softmax) 와 네거티브 샘플링 (Negative sampling) 이라는 기법을 사용할 수 있는데요. 이와 관련해서는 다음 포스팅에서 자세히 설명하도록 하겠습니다.
Word2Vec에서는 2가지 방식을 제안했는데요, Countinuous Bag of Words(CBOW) 방식과 Skip-gram 방법입니다. CBOW 모델은 주변 단어들로부터 target 단어를 예측하는 방식이고, Skip-gram 모델은 target 단어로부터 주변 단어를 예측하는 방식입니다. 빠른 이해를 위해 예제와 함께 살펴보겠습니다.
‘I am studying word2vec now’ 라는 문장에서 ‘word2vec’ 을 target 단어라고 하고 주변 단어를 target 단어의 양 옆 단어라고 정의했을 때,
CBOW 방식 : I am studying ___ now
Skip-gram 방식 : I am ___ word2vec ___
을 풀어내는 것이죠. 아래에서 CBOW와 Skip-gram 모델을 하나씩 더욱 자세히 살펴 보도록 하겠습니다.
CBOW (Countinuous Bag of Words)
CBOW의 모델 구조는 아래 그림과 같습니다. 그림에서는 window가 2인 형태로, target 단어로부터 양 옆 2개 단어까지 INPUT에 들어가도록 구성되었습니다.
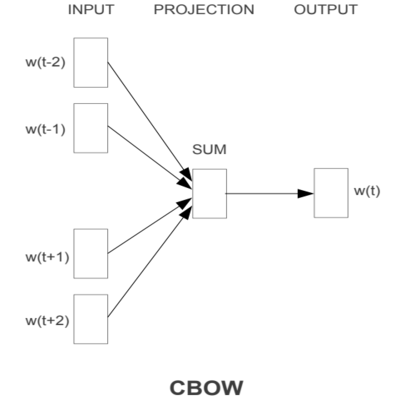
CBOW에서 주변 단어들은 동일한 weight를 공유하며 projection layer에서 합쳐집니다. Input에 들어가는 주변 단어들은 one-hot encoding 형태이기 때문에, 사실은 저번 NPLM 포스팅에서 나왔던 Table look-up 방식처럼 weight matrix로부터 자신의 인덱스에 해당하는 행만 가져오는 것이죠.
딥러닝을 위한 자연어 처리 입문에서 더욱 자세하게 설명하는 그림들이 있어 가지고 왔습니다. ‘The fat cat sat on the mat’ 이라는 예시 문장에 대해서, 아래와 같이 표현할 수 있습니다.
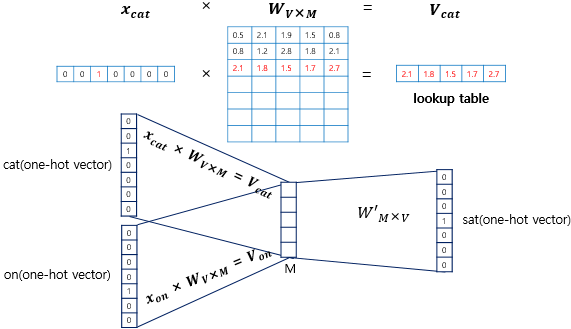
$x$는 V차원을 가지는 one-hot vector이고 $W$ matrix에서 look-up table을 통해 m차원의 vector로 임베딩이 되며, 각 주변 단어들이 모두 서로 다른 m차원의 vector로 임베딩되므로 최종적으로는 아래의 그림처럼 임베딩된 벡터들의 평균을 취해서 최종 embedded vector가 됩니다. 여기서 V는 전체 Vocabulary의 개수입니다.
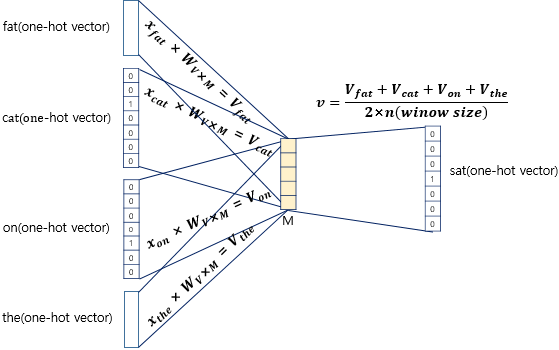
이렇게 구해진 평균 벡터는 softmax를 거쳐 target vector를 예측하기 위해 다시 W’ weight matrix와 곱해지게 됩니다.
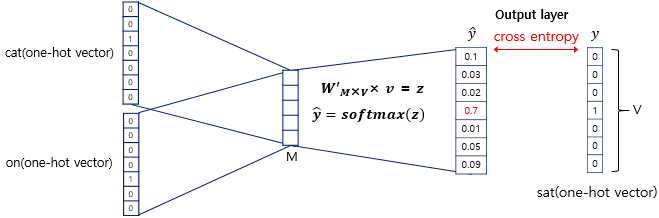
CBOW에서는 loss function으로 cross-entropy 함수를 사용하며, 수식으로 나타내면 아래와 같습니다.
\[cost(\hat{y},y) = -\sum_{j=1}^{V}y_{j}\log(\hat{y_{j}})\]그런데, target vector인 y는 one-hot vector로 encoding되어 있으므로, y = $y_{c}$(target 단어)일 때를 제외하고 모든 경우에 y = 0이 됩니다. 따라서 좀 더 간단하게 아래와 같이 표현할 수 있습니다.
\[cost(\hat{y},y) = -y_{c}\log(\hat{y_{c}}) = -1*\log(\hat{y_{c}}) = -\log(\hat{y_{c}})\]마지막으로, cost를 줄이는 방향으로 W와 W’를 최적화 해야겠죠? $ J = cost(\hat{y},y) $ 라고 했을 때,
\[J = -\log P(w_{c} | w_{c-m}, ... , w_{c-1}, w_{c+1}, ... , w_{c+m})\] \[= -\log P(u_{c} | \hat{v})\] \[= -\log \frac{\exp(u_{c}^{T} \hat{v})}{\Sigma_{j=1}^{|V|} \exp(u_{j}^{T} \hat{v})}\] \[= -u_{c}^{T} \hat{v} + \log \sum_{j=1}^{|V|} \exp(u_{j}^{T} \hat{v})\]가 됩니다. 한 줄 씩 직관적으로 풀어서 설명해보겠습니다.
첫째줄 : $\hat{y_{c}}$ 는 주변 단어들이 주어졌을 때 target 단어가 올 확률 이므로 \(P(w_{c} | w_{c-m}, ... , w_{c-1}, w_{c+1}, ... , w_{c+m})\) 로 치환됩니다.
둘째줄 : 이 확률은 결국 주변 단어들이 projection layer에서 합쳐진 평균벡터 $\hat{v}$ 가 주어졌을 때, $U$ matrix (위의 그림에서는 $W’$ matrix에 해당합니다)에서 target 단어에 대한 인덱스를 가지는 $u_{c}$가 올 확률이 되므로 치환됩니다.
셋째줄 : 또한 이 확률은 softmax를 통해 만들어진 확률이므로 softmax 함수로도 표현이 가능합니다.
넷째줄 : 수식을 보기 좋게 풀어 줍니다.
최종적으로, 우리의 목적은 J를 최소화 하는 것입니다.
대표적인 Optimize 기법인 Stochastic gradient descent (SGD)를 통해서 우리가 최적화 하고자 하는 단어 임베딩 벡터인 $W$와 $U$에 대한 편미분을 통해 gradient를 구해서 아래와 같이 업데이트 할 수 있습니다 (물론 adam과 같은 개선된 기법을 사용해도 무관합니다). 여기서 $\alpha$는 learning rate 입니다.
\[U^{(new)} = U^{(old)} - \alpha \cdot \frac{\partial{J}}{\partial{U^{(old)}}} , \quad W^{(new)} = W^{(old)} - \alpha \cdot \frac{\partial{J}}{\partial{W^{(old)}}}\]CBOW Weight Update
모델의 Weight update를 진행하려면 어떻게 해야 할까요? 먼저 update를 하고싶은 대상에 대한 gradient를 구해야겠죠. 즉, Loss function인 J에 대해서 우리가 학습시키고 싶은 parameter인 $U$와 $V$의 각 요소 ($U_{ij}$, $V_{ij}$)에 대해 편미분을 진행해야 합니다. 먼저 $U_{ij}$ 에 대한 업데이트를 해보겠습니다.
Chain rule을 사용하여 $U_{ij}$에 대한 gradient를 표현하면 아래와 같습니다.
\[\frac{\partial J}{\partial U_{ij}} = \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial U_{ij}}\]$ \frac{\partial J}{\partial z_{j}} $ 는 cross entropy의 gradient이므로 $z_{j} - y_{j}$ 로 간단히 표현할 수 있습니다.
$ \frac{\partial z_{j}}{\partial U_{ij}} = \frac{\partial (u_{j}^{T}\hat{v})}{\partial U_{ij}} = \hat{v_{i}}$ 이므로 최종적으로 $\frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial U_{ij}} = (z_{j} - y_{j}) \cdot \hat{v_{i}}$ 가 됩니다.
따라서, \(U_{ij}^{(new)} = U_{ij}^{(old)} - \alpha \cdot (z_{j} - y_{j})\cdot \hat{v_{i}}\) 로 업데이트 할 수 있습니다.
마찬가지로 Chain rule을 사용하여 $W_{ij}$에 대한 gradient를 표현하면 아래와 같습니다.
\[\frac{\partial J}{\partial W_{ij}} = \frac{\partial J}{\partial \hat{v_{i}}} \cdot \frac{\partial \hat{v_{i}}}{\partial W_{ij}}\]조금 더 부분적으로 나눠서 보도록 하겠습니다. $ \frac{\partial J}{\partial \hat{v_{i}}} $ 는 다시 $ \sum_{j=1}^{|V|} \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial \hat{v_{i}}}$ 로 분리할 수 있으며 이를 계산하면 $ \sum_{j=1}^{|V|}(z_{j}-y_{j}) \cdot U_{ij}$ 입니다.
여기서, $ \hat{v}$ 의 $i$ 번째 노드는 score layer($z$)의 모든 노드와 연결되어 있기 때문에 score layer로부터 흘러들어오는 j개의 loss를 모두 합쳐주어야 합니다. 따라서 $\Sigma$ 텀이 추가되었습니다.
다음으로, $\frac{\partial \hat{v_{i}}}{\partial W_{ij}}$ 는 $\frac{1}{C} \cdot x_{k}$로 구할 수 있는데요. 여기서 C는 주변 단어의 개수를 뜻하고 k는 input vector($x$)의 k번째 차원을 뜻합니다.
CBOW에서는 weight matrix를 공유하기 때문에 Projection layer($\hat{v}$)와 input layer 사이의 error는 총 C개의 주변단어가 projection layer로 가면서 생기는 C개의 error가 중첩됩니다. 따라서 loss를 다시 C로 나눠주어서 평균적인 에러에 대해 보정을 해주는 것이죠.
따라서, \(\frac{\partial J}{\partial W_{ij}} = \sum_{j=1}^{|V|} (z_{j}-y_{j}) \cdot U_{ij} \cdot \frac{1}{C} \cdot x_{k}\) 가 됩니다.
참고로, $x$는 one-hot vector이므로 $x_{k}$는 C개의 $x_{Ck}$ 중 단 하나만 1이 되고 나머지는 모두 0이 됩니다.
최종적으로, \(W_{ij}^{(new)} = W_{ij}^{(old)} - \alpha \cdot \sum_{j=1}^{|V|} (z_{j}-y_{j}) \cdot U_{ij} \cdot \frac{1}{C} \cdot x_{k}\) 으로 업데이트 할 수 있습니다.
Skip-gram
Skip-gram의 모델 구조는 CBOW와 반대로, Input은 target단어이므로 하나지만 output은 주변 단어이므로 여러개가 됩니다.
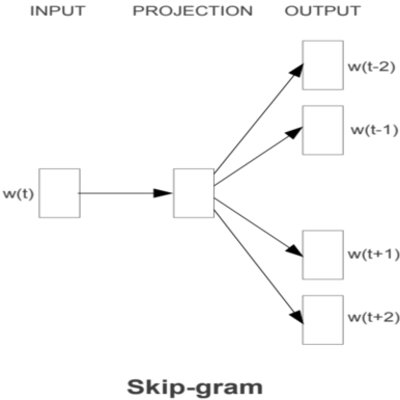
Skip-gram에서는 Input이 단어 하나이므로 projection layer에서 평균을 취하지 않고 임베딩 된 값 그대로 사용합니다. CBOW와 동일하게 one-hot vector인 $w(t)$는 weight matrix $W$에서 table-lookup을 통해 m차원의 벡터로 projection layer에 도착합니다. Skip-gram에서는 중심 단어 하나만 input으로 들어가기 때문에 CBOW처럼 projection layer에서 평균을 취하지 않아도 됩니다. 즉, skip-gram에서는 $W$ matrix의 $i$번째 행이 projection layer로 그대로 들어가게 됩니다. 아래에서 조금 더 자세히 보겠습니다.
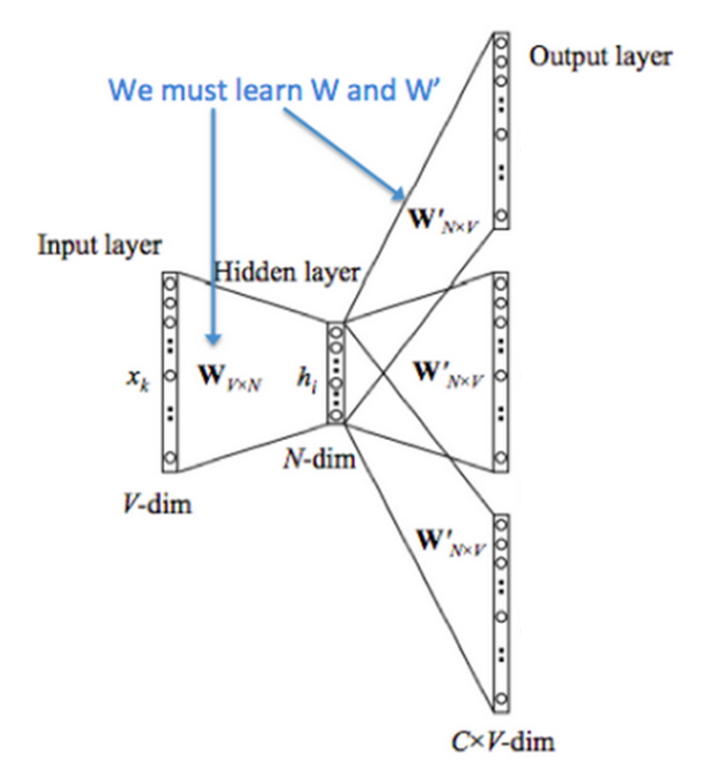
Skip-gram에서도 결국 weight matrix인 $W$와 $W’$를 학습시키는 것이 목적입니다. Skip-gram 모델에서 cost function은 어떻게 정의할 수 있을까요? CBOW의 모델의 cost function은 ‘주변 단어가 주어졌을 때 중심단어가 올 확률’ 이라는 조건부 확률을 기반으로 풀어나갔습니다. 그렇다면 skip-gram 모델에서는 반대로 ‘중심 단어가 주어졌을 때 주변 단어들이 올 확률’ 이라는 조건부 확률로 풀어나가면 되겠죠?
\[J = -\log P(w_{c-m}, ... , w_{c-1}, w_{c+1}, ... , w_{c+m} | w_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} P(w_{c-m+j} | w_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} P(u_{c-m+j} | v_{c})\] \[= -\log \prod_{j=0, j \neq m}^{2m} \frac{\exp (u_{c-m+j}^{T} v_{c})}{\sum_{k=1}^{|V|} \exp (u_{k}^{T} v_{c})}\] \[= -\sum_{j=0, j \neq m}^{2m} u_{c-m+j}^{T} v_{c} + 2m \log \sum_{k=1}^{|V|} \exp (u_{k}^{T} v_{c})\]마찬가지로 한 줄씩 풀어서 설명해보겠습니다.
첫째줄 : Cost function을 ‘중심 단어가 주어졌을 때 주변 단어가 올 확률’로 정의했습니다.
둘째줄 : Naive bayse를 이용하여 각 단어들은 서로 독립이라는 전제 하에 긴 수식을 Product를 사용하여 간결하게 표현할 수 있습니다. 여기서 $w$는 Vocabulary $V$ 안에 있는 word 입니다.
셋째줄 : 이는 결국 임베딩된 중심단어가 주어졌을 때, 임베딩된 주변 단어들이 나올 확률이므로 이렇게 쓸 수 있습니다. $v_{c}$는 $W$ matrix의 중심단어에 대한 column을 뜻하며, $u_{i}$는 $W’$ matrix의 $i$ 번째 행을 뜻합니다.
넷째줄 : 이 조건부 확률은 softmax의 확률로 대치할 수 있습니다.
마지막줄 : 넷째줄의 수식을 풀어서 써주면 됩니다.
Skip-gram weight update
다음으로, 학습을 위한 gradient를 구해 보겠습니다. 먼저, ${W’}$ matrix의 gradient부터 보겠습니다. Chain rule을 사용하면
\[\frac{\partial J}{\partial {W'}_{ij}} = \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial {W'}_{ij}}\]으로 나타낼 수 있습니다. 여기서 $z$는 output layer의 score를 뜻합니다.
one-hot vector로 표현되는 true label($y$)부터 score사이의 gradient는 cross-entropy의 gradient이므로 간단하게 score값과 label값의 차이로 구할 수 있습니다. 그런데, skip-gram 모델에서는 C개의 주변단어에 대한 cost를 구해야하므로 C개의 loss를 아래와 같이 모두 더해줍니다.
\[\frac{\partial J}{\partial z_{j}} = \sum_{n=1}^{C}(z_{j} - y_{nj})\]Output layer의 score부터 projection layer까지의 gradient는 쉽게 구할 수 있습니다.
\[\frac{\partial z_{j}}{\partial {W'}_{ij}} = h_{i}\]따라서,
\[\frac{\partial J}{\partial {W'}_{ij}} = \sum_{n=1}^{C}(z_{j} - y_{nj}) h_{i}\]가 됩니다.
다음으로, $W$ matrix에 대한 gradient를 구해 보겠습니다. 마찬가지로 Chain rule을 적용하면
\[\frac{\partial J}{\partial W_{ij}} = \frac{\partial J}{\partial z_{j}} \cdot \frac{\partial z_{j}}{\partial h_{i}} \cdot \frac{\partial h_{i}}{\partial W_{ij}}\]가 됩니다.
\(\frac{\partial z_{i}}{\partial h_{i}} = {W'}_{i}\) 이고,
\(\frac{\partial h_{i}}{\partial W_{ij}} = 1\) 이 되므로
\[\frac{\partial J}{\partial W_{ij}} = \sum_{n=1}^{C}(z_{j} - y_{nj}) W'_{i}\]가 됩니다.
최종적으로,
\[{W'}_{ij}^{(new)} = {W'}_{ij}^{(old)} - \alpha \cdot \frac{\partial J}{\partial {W'}_{ij}^{(old)}}\] \[W_{ij}^{(new)} = W_{ij}^{(old)} - \alpha \cdot \frac{\partial J}{\partial W_{ij}^{(old)}}\]으로 업데이트 할 수 있습니다.
정리 및 요약
CBOW는 ‘주변 단어로부터 중심 단어를 예측’하고, Skip-gram은 ‘중심 단어로부터 주변 단어를 예측’하는 모델임을 꼭 기억해 주시기 바랍니다.
추가로, CBOW와 Skip-gram 중 어떤 모델이 더 뛰어난 성능을 보일까요? 저는 처음 공부할 때 여러개의 주변 단어로 하나의 중심 단어를 맞추는 것이 더 쉬울 것이라고 생각해서 CBOW에 한 표를 던졌는데요. 실제로는 일반적으로 Skip-gram이 더 뛰어난 성능을 보이는 것으로 보고되어 왔고, 현재는 Word2Vec이라고 하면 자연스럽게 Skip-gram을 사용하는 것으로 통용되고 있습니다. 이번 포스팅을 완벽하게 이해하신 분들은 눈치 채셨겠지만, Skip-gram이 더 뛰어난 성능을 가지는 이유는 CBOW는 학습하는 과정에서 하나의 중심단어에 대한 error를 구하고 update를 하지만, Skip-gram에서는 여러개의 주변단어에 대한 error들을 구하고 각각 update를 하기 때문입니다.
마치며
이번 포스팅에서는 NLP의 역사에서 큰 부분을 차지하고 있는 Word2Vec을 공부했기 때문에 기본 개념부터 시작해서 weight update 까지 깊이 공부해 보았습니다. 수식들을 다루느라 저도 여러 자료들을 참고하며 정리를 해보았는데요, 혹시 틀린 부분이 있다면 해당 부분에 대해서 피드백 주시면 정말 감사하겠습니다.
또 하나, 실제 Word2Vec에서는 연산량을 줄이고 효율적으로 학습하기 위한 2가지 방법, 계층적 소프트맥스 (Hierarchical softmax) 와 네거티브 샘플링 (Negative sampling)이 적용 되고 있습니다.
다음 포스팅에서는 이 2가지 방법에 대해서 자세하게 다루어보도록 하겠습니다.
References
Baek Kyun Shin 님의 블로그
딥러닝을 이용한 자연어 처리 입문
Inhwan Lee 님의 블로그
Alex Minnaar’s Blog
Xin Rong’s arxiv

Comments