Word2vec 2편 Word2vec 개선 방법들
안녕하세요, 저번 포스팅에서는 Word2Vec에 대한 기초 개념부터 weight update까지 다루어보았는데요. 이번 포스팅에서는 Word2Vec에서 연산량을 줄이기 위한 개선 방법들을 소개하려고 합니다. 이 개선 방법들은 2013년 구글에서 Distributed Representations of Words and Phrases and their Compositionality 라는 제목으로 발표한 논문에서 다루고 있습니다.
이번 포스팅에서는 Word2Vec의 2가지 방법 중 Skip-gram에 초점을 맞추어 작성 하도록 하겠습니다.
특히, 이번 포스팅은 BEOMSU KIM님과 Inwhan Lee 님의 블로그에서 설명을 정말 잘 해주셔서 많은 참고를 했음을 미리 알려드립니다 (맨 아래 reference에 해당 링크가 있습니다).
Background
Word2Vec은 NPLM의 hidden layer를 과감히 제거하여 연산량을 크게 줄였습니다. 하지만, Vocabulary 안의 단어 수가 10만개, 100만개로 늘어난다면 연산량 또한 기하급수적으로 늘어날 수 밖에 없습니다.
이를 해결하기 위한 2가지 방법이 있는데요, 바로 계층적 소프트맥스(Hierarchical Softmax 와 네거티브 샘플링(Negative sampling) 입니다.
하나씩 살펴보도록 하겠습니다.
계층적 소프트맥스 (Hierarchical Softmax)
Vocabulary의 단어 수가 많아졌을 때 가장 연산량을 많이 잡아먹는 부분은 Softmax부분입니다. Vocabulary가 가지고 있는 단어의 수(V)만큼의 score에 대해서 일일이 계산을 하여 총 합이 1이 되도록 만들어야 하기 때문이죠. 이를 방지하기 위해서 Softmax 대신 binary tree를 이용한 multinomial distribution function(다항분포함수)을 사용 합니다.
먼저, 아래와 같이 모든 단어들을 binary tree를 이용하여 표현한다고 해봅시다. tree의 각 잎(leaf, 트리의 말단)은 각 단어이며, 가장 위에 있는 노드인 뿌리(root)로부터 각 잎까지는 유일한 경로(path)로 연결됩니다.
Hierarchial Softmax를 사용할 경우 기존 CBOW나 Skip-gram에 있던 $W’$ matrix를 사용하지 않습니다. 대신, V-1개의 internal node(내부 노드)가 각각 길이 N짜리 weight vector를 가지게 됩니다. 이를 $v’_{i}$ 라고 하고 학습을 통해 update 합니다.
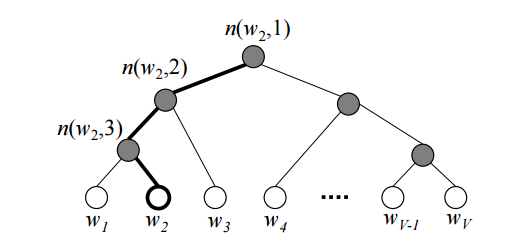
Notations
내용을 본격적으로 설명하기 전에, 사용되는 notation들에 대해 먼저 설명 드리겠습니다.
n(w2,2) : 뿌리(root)부터 w2까지 가는 경로(path) 중 2번째로 만나는 노드
L(w2) : 뿌리(root)부터 w2까지 가는 경로(path)의 길이
ch(node) : 특정 node에서의 고정된 임의의 한 자식(child)
[[x]] : x가 true일 경우 1, false일 경우 -1을 반환하는
h : projection layer의 vector
${v’}_{i}$ : 각 Internal node(내부 노드)가 가지는 N차원의 weight vector
$\mathbf{\sigma(x)}$ : sigmoid function ( $ \frac{1}{1+\exp(-x)})$
Equation
Tree를 이용한 확률에 대한 수식을 살펴보겠습니다. 임의의 단어 $w$가 주변 단어 $w_{O}$가 될 확률은 아래와 같이 정의됩니다.

위의 수식에서 $\sigma$ 함수 안을 살펴 봅시다. \(n(w, j+1) = ch(n(w,j))\)
위 식은 Tree 내의 특정 노드 (즉, 뿌리부터 단어 w까지 가는 경로에서 j+1번째 노드)가 바로 위에 있는 노드(뿌리부터 단어 w까지 가는 경로에서 j번째 노드)의 고정된 child냐는 뜻입니다.
다시 말해서, $n(w,j)$ 노드에서 왼쪽으로 가는 경우와 오른쪽으로 가는 경우에 따라 $\sigma$ 함수 안은
${v’}^{T}_{n(w,j)} h$ 또는
${-v’}^{T}_{n(w,j)} h$ 가 되는 것이죠.
${v’}_{n(w,j)}^{T} h = x$ 로 치환하면, 결국 $\sigma(x)$ 또는 $\sigma(-x)$ 가 됩니다.
특정 노드에서 왼쪽으로 가거나 오른쪽으로 가는 두 가지 선택지의 합을 나타내면 $\sigma(x) + \sigma(-x)$인데요, Sigmoid 함수는 $\sigma(x) + \sigma(-x) = 1$ 을 만족하는 특징이 있습니다.
따라서 Tree 안의 모든 node가 이 관계를 만족하게 되므로, 뿌리부터 각 단어들까지 가는 경로들의 전체 합도 1이 됩니다. 최종적으로 확률 분포를 이루게 되는 것이죠. 이를 수식으로 나타내면 아래와 같습니다.
\[\sum_{w=1}^{V} p(w | w_{c}) = 1\]위 수식은 중심단어 $ w_{c} $ 가 주어졌을 때 Vocabulary 안의 특정 단어 $w$가 올 확률들을 모두 더하면 1이라는 뜻입니다.
이와 같이 binary tree를 이용하여 Softmax를 대체할 수 있으며, 손실함수는 동일하게 cross-entropy를 적용하여
\[J = -\log p(w | w_{i})\]로 정의할 수 있습니다.
논문에 따르면 손실함수의 gradient를 구하는 과정에서의 연산량은 $L(w_{o})$에 비례하며, 최대 $\log$ V 의 연산량을 가지고, 평균적으로는 $\log_{2}$ V 의 연산량을 가지게 된다고 합니다. 기존의 V 만큼의 연산량에 비해서는 획기적으로 줄어들게 됩니다.
원문에서는 Huffman tree를 이용하여 계층적 소프트맥스(Hierarchial Softmax)를 구현했습니다. Huffman tree를 이용하면 빈도가 높은 단어일수록 뿌리와 가깝게 생성되므로 실질적인 연산량을 더욱 줄일 수 있을 것 같네요.
네거티브 샘플링 (Negative Sampling)
Hierarchial 대신 사용할 수 있는 또 하나의 방법으로 Negative Sampling이 있습니다.
Nagetive Sampling의 핵심 아이디어는, Softmax를 Vocabulary의 전체 단어에 적용하려고 하니 연산량이 너무 많으므로, 일부만 샘플링하여 Softmax를 계산하자! 입니다. 기존에 V만큼의 연산량을 샘플링한 개수인 K만큼으로 줄일 수 있게 되는 것이죠.
그렇다면 어떤 식으로 샘플링을 하고, 학습을 시켜야 할까요? 주변단어와 중심단어를 positive samples라고 하고, 그 외의 단어들을 negative samples라고 합시다. positive samples와 negative samples를 합쳐 총 k개의 단어를 샘플링 합니다.
\[Samples = \{w_{1}, ... , w_{k}\}\]중심단어를 $c$ , 주변 단어를 $o$ , negative samples에 해당하는 단어를 $w_{i}$ 라고 합시다. 우리의 학습 목표는 $p(o | c)$ 는 증가시키고 $p(w_{i} | c)$ 는 감소시키는 방향으로 모델을 훈련시키는 것이 됩니다.
다시 말해서, $p(o|c)$ 와 $ 1 - p(w_{i}|c) $ 를 둘 다 증가시키면 되는 것이죠. 이를 수식으로 나타내면 아래와 같습니다.
\[maximize (\log (\,\, p(o|c) \cdot \prod_{i=1}^{k} (1- p(w_{i}|c)))\] \[= maximize \, (\, \log p(o|c) + \sum_{i=1}^{k} \log (1-p(w_{i} | c)))\]다음으로, 중심단어에 대해 단어 w가 올 확률을 Sigmoid 함수를 사용하여 아래와 같이 정의할 수 있습니다.
\[p(w|c) := \sigma(u_{w}^{T} v_{c})\]여기서 $u_{w}$는 $W’$ weight matrix의 w번째 행에 해당하는 벡터이고, $v_{c}$는 중심단어가 $W$ matrix를 통해 임베딩된 벡터이자 projection layer의 벡터이기도 합니다. 시그모이드 함수는 $ 1 - \sigma(x) = \sigma(-x)$ 를 만족하므로 우리의 목표 함수 (Objective function)를 다시 쓰면,
\[maximaze \, ( \log \sigma(u_{o}^{T} v_{c}) + \sum_{i=1}^{K} \log \sigma(-u_{w_{i}}^{T} v_{c}))\]가 됩니다.
따라서, 손실함수는 아래와 같습니다.
\[J := -\log \sigma(u_{o}^{T} v_{c}) - \sum_{i=1}^{K} \log \sigma(-u_{w_{i}}^{T} v_{c})\]위 손실함수를 기반으로 gradient를 계산하여 weight를 업데이트 할 수 있습니다.
Sampling 방법
지금까지 Negative sampling의 방법에 대해서 공부를 해봤는데요. 그렇다면 샘플링을 어떻게 했을 때 가장 효과적일까요? 보통 샘플링은 전체 데이터셋에서 각 데이터가 등장하는 빈도를 이용하여 확률적으로 샘플링을 진행하지만, 텍스트 데이터 특성상 자주 등장하는 단어와 그렇지 않은 단어의 빈도 차이가 극심하기 때문에, 자주 등장하지 않는 단어는 샘플링에서 거의 배제될 가능성이 있습니다. 따라서, Negatve sampling에서는 아래와 같은 확률 분포를 이용하여 샘플링을 합니다.
\[p(w) = \frac{f(w)^{n}}{\sum_{w} f(w)^{n}}\]위 식은 unigram model을 기반으로 하며, 여기서 f(w)는 단어 w의 빈도를 뜻합니다.
논문 저자에 따르면 데이터가 작을 경우 k = 5 ~ 25 사이에서, 클 경우는 k = 2 ~ 5 사이의 값을 선택 했을 때 실험결과가 좋았으며, n = 3/4를 적용했을 때 실험결과가 가장 좋다고 합니다.
예를 들어서 조금 더 쉽게 설명하면, [A, A, A, A, B] 라는 데이터셋이 있을 때, A가 나올 확률은 0.8이고 B가 나올 확률은 0.2 입니다.
조정된 확률로 계산하면 $ \frac{(0.8)^{3/4}}{(0.8)^{3/4}+(0.2)^{3/4}} = 0.738$, $ \frac{(0.2)^{3/4}}{(0.8)^{3/4}+(0.2)^{3/4}} = 0.261$ 으로, 단어 간의 빈도차이를 조정하여 골고루 샘플링이 되도록 해줍니다.
Subsampling of Frequent Words
Hierarchical Softmax와 Negative Sampling은 기존 Softmax 방법의 연산량을 줄이기 위한 테크닉이었습니다. 추가적으로, 논문에서는 'the', 'a', 'is'와 같은 자주 등장하지만 크게 의미는 없는 단어들을 확률적으로 제외하여 학습속도와 성능을 모두 향상시켰습니다.
단어의 등장 빈도를 $f(w)$라고 했을 때,
\[P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}}\]의 확률로 제거하는 방법입니다.
여기서 t는 threshold 값으로, 실험적으로 $10^{-5}$의 값을 사용했을 때 가장 좋은 결과를 얻었다고 합니다.
Learning Phrases
또 하나, 논문에서 다루는 개선 방법이 있습니다. 텍스트 데이터를 다룰 때는 보통 단어 단위로 토큰화(Tokenization)하여 단어의 벡터화를 진행합니다. 그런데, New York Times 와 같은 고유명사는 New, York, Time 각각의 단어가 가지고 있는 의미와는 완전히 다른 의미이므로, 하나의 명사로서 취급을 해주어야합니다. 하지만, This is 와 같은 구절은 함께 자주 쓰이기는 해도 새로운 의미가 생기지는 않습니다.
이처럼 여러개의 단어가 모여서 고유명사를 이루는 경우를 토큰화 해주기 위해서 논문에서는 별도의 score 기준을 아래와 같이 제안했습니다.
\[score(w_i, w_j) = \frac{f(w_i w_j) - \delta}{f(w_i) f(w_j)}\]여기서 $f(w_i)$는 단어 $w_i$의 빈도이고, $f(w_i w_j)$는 두 단어가 연속으로 발생하는 빈도를 뜻합니다. 이상적으로는 두 단어가 아니라 n개의 단어까지 연속으로 발생하는 빈도를 구해야겠지만, 현실적으로는 메모리 등의 제약이 있어 본 논문에서는 unigram과 bi-gram모델까지만 고려했습니다.
두 단어로 이루어진 고유 명사라면 각각 존재하는 확률보다 함께 존재할 확률이 높으므로 score가 높게 나오게 되는 것이죠.
그런데, 두 단어 고유명사가 아니지만 그냥 발생횟수 자체가 적어서 score가 높게 나오는 경우도 있습니다. 이를 방지하기 위해서 $\delta$라는 요소를 넣어 적정 빈도 이하로 발생하는 조합은 고유명사로 고려하지 않도록 했습니다.
하지만, 그렇다고 해서 3개 이상의 단어로 이루어진 고유 명사를 아예 토큰화하지 못하는 것은 아닙니다.
가령, Samsung Electronic Pad라는 단어가 위 학습에 의해 Samsung Electronic와 Electronic Pad 두 고유명사로 학습이 되었다고 합니다. 한번 더 학습을 수행하면 이 두 고유명사가 각각 개별 단어로 만나서Samsung Electronic Pad라는 고유명사까지 토큰화가 될 수도 있습니다.
마치며
이번 포스팅에서는 Word2Vec의 연산량과 몇몇 이슈들을 해결하고 개선하기 위한 방법들을 공부했습니다. NLP 역사에 한 획을 그은 기법인만큼, 시간이 좀 걸리더라도 최대한 꼼꼼하게 공부하려고 노력했습니다. 하지만, 백논문은 불여일코딩 이라고, 이론적으로 이해했으니 반드시 구현을 하면서 체화시키는 과정이 필요합니다.
다음 포스팅에서는 pytorch를 기반으로 Word2Vec의 skip-gram 모델을 직접 구현해보고자 합니다. 가능하다면 negative sampling까지 적용해서 구현을 해보도록 하겠습니다.
긴 글 읽어주셔서 감사드리며, 다음 포스팅에서 뵙겠습니다 !

Comments