VQ-Wav2vec 논문 꼼꼼 리뷰 - 1편
VQ-Wav2vec: Self-supervised learning of discrete speech representations
ABSTRACT
VQ-Wav2vec 은2020년 Facebook에서 발표한 논문으로, 기존 Wav2vec 모델에 discrete representation을 추가하여 NLP community에서 요구하는 discrete inputs 조건을 만족할 수 있도록 발전시킨 모델입니다. VQ는 Vector quantized의 약자입니다.
Discrete input을 사용하는 대표적인 모델로는 BERT가 있으며, 본 논문에서도 BERT의 MLM(Masked Language Model) pre-training 기법을 도입하여 TIMIT phoneme classification과 WSJ speech recognition에서 new SOTA(State-of-the-art)를 달성했습니다.
본 포스팅은 Wav2vec에 대한 배경지식이 없으면 이해하기가 다소 힘들 수 있습니다. Wav2vec에 대한 자세한 내용이 궁금하신 분은 이전 포스팅을 참고하시면 되겠습니다 :)
INTRODUCTION
본 논문에서는 speech 분야에서 discrete representation을 학습하는 것과 self-supervised 기반의 speech representation을 학습하는 방법(Wav2vec), 두 마리 토끼를 잡기위해 Wav2vec 모델에 discretization(이산화) 기법을 추가했습니다. discrete representaion을 통해 BERT와 같은 well-performing NLP 알고리즘에 speech 데이터를 적용할 수도 있게 되었구요.
저자들은 discrete representation을 만들기 위해서 Gumbel-softmax와 K-mean clustering 기법을 적용했습니다. 다음으로, 저자들은 discrete representation을 BERT 모델의 Input으로 사용하여 MLM(Masked language modeling) 기반 훈련을 시켰습니다. 최종적으로 훈련을 마친 BERT의 output으로 나온 representation을 acoustic model의 input으로 사용하여 supervised speech recognition의 성능을 향상시켰습니다. Discretization 기법과 MLM에 대한 자세한 설명은 잠시 후 모델 설명과 함께 하도록 하겠습니다.
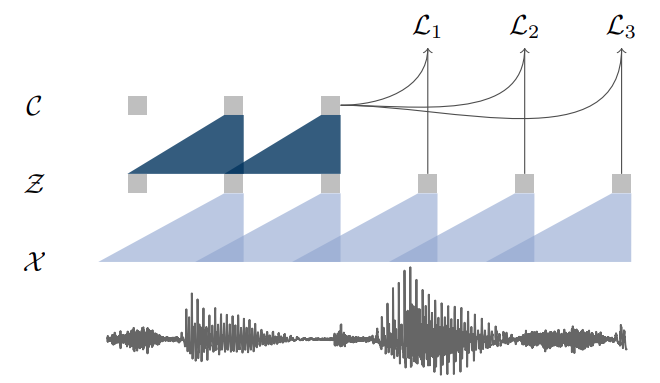
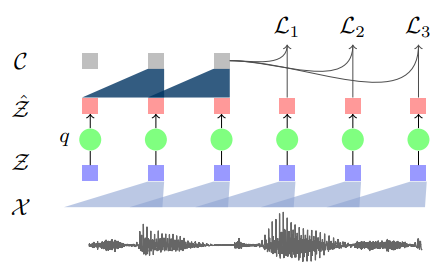
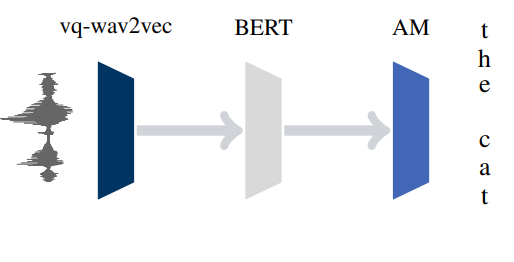
먼저, 모델 비교 그림부터 보겠습니다. 왼쪽에 있는 기존 Wav2vec 모델 구조에서 quantization 모듈(q)과 discrete representation(Ẑ)이 추가된 것을 알 수 있습니다. 다음으로, 파이프라인 그림을 보면 위에서 언급한대로 VQ-Wav2vec, BERT, Acoustic model 순서로 나열되어 있습니다. 이는 각 3개의 모델이 순차적으로 학습되고, 최종적으로 AM에서 나온 output을 이용해 supervised speech recognition task를 하도록 구성된 것을 것을 잘 보여주고 있습니다.
VQ-Wav2vec
Model
Encoder network ( f : X -> Z )
VQ-Wav2vec은 Wav2vec과 동일하게 Raw audio(X) 신호부터 시작합니다. 16KHz 오디오 신호의 30ms 구간에서 하나의 feature representation(Z)을 생성하며, 10ms의 stride를 가지고 진행합니다. raw audio signal을 feature representation으로 인코딩하기 위해 8-layer convolutional network로 구성했는데요, wav2vec에서는 5-layer였던 것과 비교하면 사이즈가 조금 커진것을 확인할 수 있습니다. 각 layer의 kernel size는 (10, 8, 4, 4, 4, 1, 1, 1)이고 stride는 (5, 4, 2, 2, 2, 1, 1, 1)입니다.
Quantization module (q: Z -> Ẑ)
VQ-Wav2vec의 핵심이 되는 quantization module입니다. Quantization 모듈은 feature representation(Z)를 discrete representation(Ẑ)로 바꿔주는 역할을 합니다. 이를 위해 고정된 크기의 Codebook(Embedding matrix)을 사용하며, codebook은 d 크기를 갖는 V개의 representation으로 구성되어 있습니다 ( e ∈ RV ×d ).
이 codebook으로부터 벡터 하나를 뽑아서 쓰면 discrete representation이 만들어집니다 ( Ẑ = ei). Codebook으로부터 벡터를 뽑는 가장 쉽고 직관적인 방법은 V 크기의 벡터에 argmax를 적용해서 최댓값의 인덱스를 사용하는 것입니다. 그러나, argmax는 미분 불가능한 함수이기 때문에 backpropagation을 진행할 수 없습니다. 따라서, 저자들은 argmax와 같은 역할을 하면서도 미분이 가능한 함수로 Gumbel-softmax와 K-mean clustering을 제안했습니다.
Gumbel-Softmax
Gumbel-Softmax를 통해 이산화(discretization)를 하는 과정을 좀 더 구체적으로 살펴보겠습니다. 먼저, feature representation(Z)에 linear layer와 비선형성을 위한 ReLU를 적용한 후, output이 l ∈ R V 인 logit으로 나올 수 있도록 또 다른 linear layer를 적용합니다. 다음으로, 0부터 1까지의 범위를 갖는 uniform distribution으로부터 V개의 sample을 뽑아 벡터 u를 만듭니다. 뽑힌 u에 log를 취해 v를 만듭니다.
\[v = − log(− log(u))\]logit(l)과 v를 더한 후에, softmax를 취해주면 Codebook 안의 총 V개의 representation 중 j번째 representation을 뽑을 확률이 아래와 같이 정의됩니다.
\[p_{j} = \frac{exp(l_{j} + v_{j} )/τ}{\Sigma_{k=1}^V exp(l_{k} + v_{k})/τ} l_{t}\]여기서 τ는 temperature로, τ가 작을수록 p의 분포가 이산 분포에 가까워집니다. 이를 통해 Discrete representation으로 근사할 때 유연성을 줄 수 있습니다.
실제 구현에서는 효율성을 위해서 forward propagation은 그냥 argmax를 취하고, backpropagation을 할 때만 Gumbel-Softmax의 true gradient output을 넘겨주도록 했다고 합니다.
K-Means clustering
이산화를 하는 두 번째 방법은 K-means clustering을 활용한 방법입니다. Codebook 안의 vector들에 각 index를 부여한 후에, feature representation(Z)와 가장 거리가 가까운 index를 찾는 방식이며, 이때 거리 척도로 유클리디안 거리를 사용합니다.

K-means clustering에서도 미분이 불가능한 argmin 함수가 들어 있기 때문에, backpropagation 시 gradiendt가 흐를수 있게 구현상에 Trick을 추가했습니다.
def _pass_grad(self, x, y):
""" Manually set gradient for backward pass.
for y = f(x), ensure that during the backward pass,
dL/dy = dL/dx regardless of f(x).
Returns:
y, with the gradient forced to be dL/dy = dL/dx.
"""
return y.detach() +(x - x.detach())
K-means clustering을 사용할 때에는, Codebook의 벡터도 함께 학습시키기 위해 최종 Loss에 2가지 Term을 추가합니다.

첫 번째 Term에서는 codebook의 vector에만 gradient가 흐르기 때문에 codebook의 vector(Ẑ)가 feature representation(Z)이랑 가까워지도록 하는 역할을 합니다. 이와 비슷하게, 두 번째 Term에서는 feature representation(Z)에만 gradient가 흐르기 때문에 feature representation(Z)이 codebook의 vector(Ẑ)와 가까워지도록 합니다.
Context network ( f : Ẑ -> C )
Context network에서는 discrete representation을 aggregation하여 context를 만듭니다. 이렇게 만들어진 context를 이용하여 기존 Wav2vec과 동일한 방식으로 contrastive learning을 통해 학습합니다.
Implementation Details
지금까지 Codebook을 활용하여 discrete representation을 만들어내는 방법들을 살펴 보았는데요. 사실 실제 구현에서는 디테일이 조금 더해져야 합니다. 만약 위에서 설명한대로 Codebook에서 벡터들을 뽑게 되면, 벡터가 골고루 뽑히지 않고 특정 벡터들만 뽑히는 mode collapse 경향이 발생하게 됩니다. 이를 해결하기 위해 Codebook을 re-initializing하거나 loss function에 추가적인 regularizer를 적용하는 등의 사전연구들이 있었습니다.
본 연구에서는 새로운 방법을 제시했습니다. d의 크기를 갖는 feature representation vector(z)를 여러개의 Group으로 쪼개는 방식입니다.
\[z ∈ R^{d} ⟶ z' ∈ R^{G \times \frac{d}{G}}\]가령, d=8차원의 벡터에 대해 G=2개의 Group으로 쪼개면 4차원의 벡터가 2개 생기는 것이죠. 이렇게 할 경우 기존 feature representation vector(z)를 나타내기 위해서는 G개의 인덱스가 필요하게 됩니다. Quantization을 수행할 때에는 각 그룹별로 정수 인덱싱을 한 후에, 각 그룹에서 Gumbel-softmax나 K-means clustering을 통해 하나씩 인덱싱을 합니다.
그렇다면 Codebook의 차원은 어떻게 될까요? codebook도 두가지 방식으로 생각을 해볼 수 있습니다. 첫 번째는 각 Group이 하나의 codebook을 공유하는 경우입니다. 이 경우, codebook의 차원은 e ∈ RV × (d/G)가 됩니다. 만약 각 group에 대해 codebook을 독립적으로 만든다면, 전체 codebook의 차원은 e ∈ RG x V × (d/G)가 됩니다. 최종적으로, 각 group에서 얻은 G개의 d/G차원 벡터들을 concatenate하면 d차원의 discrete representation(Ẑ)이 만들어지게 됩니다.
여기까지 VQ-wav2vec의 모델에 대해서 알아보았습니다. 다음 포스팅에서는 VQ-wav2vec을 훈련한 후에, quantized 정보를 활용하여 BERT를 훈련시키는 부분과 최종 모델의 experiment 및 성능에 대해서 알아보도록 하겠습니다.
Reference
VQ-Wav2vec : Self-Supervised Learning of Discrete Speech Representations

Comments